DS-Stack and Queue

4 minute read

Published: March 09, 2025

接着复习408基础知识，今天是数据结构与算法的栈和队列。栈和队列都是一种操作首先的线性表。

（一）栈

1、基本概念

栈：是只允许在一端进行插入或删除的线性表。首先栈是一种线性表只能在某一端进行插入和删除操作。栈又称为后进先出（Last In First Out）的线性表，简称LIFO结构

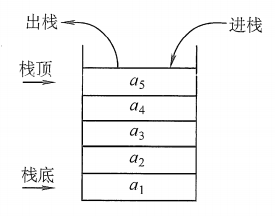
在这里插入图片描述

栈顶（Top）：线性表允许进行插入删除的那一端。

栈底（Bottom）：固定的，不允许进行插入和删除的另一端。

空栈：不含任何元素的空表。

2、栈的存储结构

因为是线性标的一种，也分为顺序存储和链式存储。

（1）静态顺序存储

#define MaxSize 100
#define int ElemType 
typedef struct
{ ElemType data[MaxSize]; // 数组存储空间
  int top;   //栈顶下标
} SqStack;  // 顺序栈数据类型

MaxSize为顺序栈的最大容量

top为栈顶元素的下标，0 <= top <= MaxSize-1

栈空：top = -1

栈满：top = MaxSize-1

在这里插入图片描述

初始化

void InitStack(SqStack *S){
    S->top = -1;    //初始化栈顶指针
}

判空

bool StackEmpty(SqStack S){
    if(S.top == -1){    
        return true;    //栈空
    }else{  
        return false;   //不空
    }
}

进栈（push）

/*插入元素e为新的栈顶元素*/
Status Push(SqStack *S, ElemType e){
    //满栈
    if(S->top == MAXSIZE-1){
        return ERROR;
    }
    S->top++;   //栈顶指针增加一
    S->data[S->top] = e;    //将新插入元素赋值给栈顶空间
    return OK;
}

出栈（pop）

/*若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK；否则返回ERROR*/
Status Pop(SqStack *S, ElemType *e){
    if(S->top == -1){
        return ERROR;
    }
    *e = S->data[S->top];   //将要删除的栈顶元素赋值给e
    S->top--;   //栈顶指针减一
    return OK;
}

读栈顶元素

/*读栈顶元素*/
Status GetTop(SqStack S, ElemType *e){
    if(S->top == -1){   //栈空
        return ERROR;
    }
    *e = S->data[S->top];   //记录栈顶元素
    return OK;
}

* 共享栈

利用栈底位置相对不变的特征，可让两个顺序栈共享一个一维数组空间，将两个栈的栈底分别设置在共享空间的两端，两个栈顶向共享空间的中间延伸。

在这里插入图片描述

两个栈的栈顶指针都指向栈顶元素，top0 = -1时0号栈为空，top1 = MaxSize时1号栈为空。
仅当两个栈顶指针相邻top0 + 1 = top1时，判断为栈满。
当0号栈进栈时top0先加1再赋值；1号栈进栈时top1先减一再赋值。出栈时则刚好相反。

构建共享栈

/*两栈共享空间结构*/
#define MAXSIZE 50  //定义栈中元素的最大个数
typedef int ElemType;   //ElemType的类型根据实际情况而定，这里假定为int
/*两栈共享空间结构*/
typedef struct{
    ElemType data[MAXSIZE];
    int top0;    //栈0栈顶指针
    int top1;    //栈1栈顶指针
}SqDoubleStack;

共享栈进栈

对于两栈共享空间的push方法，我们除了要插入元素值参数外，还需要有一个判断是栈0还是栈1的栈号参数stackNumber。

/*插入元素e为新的栈顶元素*/
Status Push(SqDoubleStack *S, Elemtype e, int stackNumber){
    if(S->top0+1 == S->top1){   //栈满
        return ERROR;
    }
    if(stackNumber == 0){   //栈0有元素进栈
        S->data[++S->top0] = e; //若栈0则先top0+1后给数组元素赋值
    }else if(satckNumber == 1){ //栈1有元素进栈
        S->data[--S->top1] = e; //若栈1则先top1-1后给数组元素赋值
    }
    return OK;
}

共享栈出栈

直接分开讨论空栈情况。

/*若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK；否则返回ERROR*/
Status Pop(SqDoubleStack *S, ElemType *e, int stackNumber){
    if(stackNumber == 0){
        if(S->top0 == -1){
            return ERROR;   //说明栈0已经是空栈，溢出
        }
        *e = S->data[S->top0--]; //将栈0的栈顶元素出栈，随后栈顶指针减1
    }else if(stackNumber == 1){
        if(S->top1 == MAXSIZE){
            return ERROR;   //说明栈1是空栈，溢出
        }
        *e = S->data[S->top1++];    //将栈1的栈顶元素出栈，随后栈顶指针加1
    }
    return OK;
}

（2）链式存储

采用链式存储的栈称为链栈，链栈的优点是便于多个栈共享存储空间和提高其效率，且不存在栈满上溢的情况。通常采用单链表实现，并规定所有操作都是在单链表的表头进行的。

同时，为了操作方便，使用不带头节点的单链表来实现链表。

数据类型定义

typedef struct LinkNode{
    int data;//数据域
    struct LinkNode *next;//指针域 
}stackNode,*LinkStack; 

stackNode是struct LinkNode的别名，也就是说，stackNode可以直接用来声明该结构体类型的变量。 LinkStack是指向struct LinkNode的指针的别名，常用来表示链栈的栈顶指针或链表的头指针。

初始化

直接把头指针设为NULL。

void initStack(LinkStack &s)
{
    s=NULL;//不需要头节点 
}

入栈

判断头指针是否为空

int stackEmpty(LinkStack s)
{
    if(s==NULL)
        return 1;
    return 0;
}

判断栈内元素数量

int stackLength(LinkStack s)
{
    int sum=0;
    stackNode *temp=s;
    while(temp!=NULL)
    {
        sum++;
        temp=temp->next;
    }
    return sum;
}

入栈

void push(LinkStack &s,int e)
{
    stackNode *p=new stackNode;
    p->data=e;
    p->next=NULL;
    if(s==NULL)
        s=p;
    else
    {
        p->next=s;
        s=p;
    }
}

出栈

void pop(LinkStack &s,int &e)
{
    stackNode *p=new stackNode;
    if(s==NULL)
    {
        cout<<"栈为空，无法弹出"<<endl;
    }
    else
    {
        p=s;
        e=p->data;
        s=s->next;
        delete p;
        cout<<"成功弹出栈顶元素"<<endl;
    }
}

栈顶元素

int top(LinkStack s)
{
    if(s==NULL)
        return -1;
    return s->data;
}

3、栈的运用

递归
四则运算表达式

（二）队列

1、基本概念

队列（queue）是只允许在一端进行插入操作，而在另一端进行删除操作的线性表。

队列是一种先进先出（First In First Out）的线性表，简称FIFO。允许插入的一端称为队尾，允许删除的一端称为队头。

在这里插入图片描述

2、队列的顺序存储结构

队列的顺序实现是指分配一块连续的存储单元存放队列中的元素，并附设两个指针：队头指针front指向队头元素，队尾指针rear指向队尾元素的下一个位置。

（1）顺序队列

队列的顺序存储类型可描述为:

#define MAXSIZE 50    //定义队列中元素的最大个数
typedef struct{
    ElemType data[MAXSIZE];    //存放队列元素
    int front,rear;
}SqQueue;

初始状态（队空条件）：Q->front == Q->rear == 0。进队操作：队不满时，先送值到队尾元素，再将队尾指针加1。出队操作：队不空时，先取队头元素值，再将队头指针加1。

在这里插入图片描述

如图(d)，队列出现“上溢出”，然而却又不是真正的溢出，所以是一种“假溢出”。

（2）循环队列

解决假溢出的方法就是后面满了，就再从头开始，也就是头尾相接的循环。我们把队列的这种头尾相接的顺序存储结构称为循环队列。当队首指针Q->front = MAXSIZE-1后，再前进一个位置就自动到0，这可以利用除法取余运算（%）来实现。

初始时：Q->front = Q->rear=0。队首指针进1：Q->front = (Q->front + 1) % MAXSIZE。队尾指针进1：Q->rear = (Q->rear + 1) % MAXSIZE。队列长度：(Q->rear - Q->front + MAXSIZE) % MAXSIZE。出队入队时，指针都按照顺时针方向前进1，如下图所示：

在这里插入图片描述

那么，循环队列队空和队满的判断条件是什么呢？显然，队空的条件是Q->front == Q->rear（初始条件就是 Q->front = Q->rear = 0）。若入队元素的速度快于出队元素的速度，则队尾指针很快就会赶上队首指针，如图( d1 ）所示，此时可以看出队满时也有 Q ->front == Q -> rear 。为了区分队空还是队满的情况，有三种处理方式：

牺牲一个单元来区分队空和队满，入队时少用一个队列单元，这是种较为普遍的做法，约定以“队头指针在队尾指针的下一位置作为队满的标志”，如图 ( d2 ）所示。
- 队满条件： (Q->rear + 1)%Maxsize == Q->front
- 队空条件仍： Q->front == Q->rear
- 队列中元素的个数： (Q->rear - Q ->front + Maxsize)% Maxsize
类型中增设表示元素个数的数据成员。
- 队空的条件为 Q->size == O
- 队满的条件为 Q->size == Maxsize 。
类型中增设tag 数据成员，以区分是队满还是队空。
- tag 等于0时，若因删除导致 Q->front == Q->rear ，则为队空
- tag 等于 1 时，若因插入导致 Q ->front == Q->rear ，则为队满。

针对第一种方法构建循环队列：

数据类型

typedef int ElemType;   //ElemType的类型根据实际情况而定，这里假定为int
#define MAXSIZE 50  //定义元素的最大个数
/*循环队列的顺序存储结构*/
typedef struct{
    ElemType data[MAXSIZE];
    int front;  //头指针
    int rear;   //尾指针,若队列不空，指向队列尾元素的下一个位置
}SqQueue;

初始化

/*初始化一个空队列Q*/
Status InitQueue(SqQueue *Q){
    Q->front = 0;
    Q->rear = 0;
    return OK;
}

判空

/*判队空*/
bool isEmpty(SqQueue Q){
    if(Q.rear == Q.front){
        return true;
    }else{
        return false;
    }
}

返回长度

/*返回Q的元素个数，也就是队列的当前长度*/
int QueueLength(SqQueue Q){
    return (Q.rear - Q.front + MAXSIZE) % MAXSIZE;
}

入队

/*若队列未满，则插入元素e为Q新的队尾元素*/
Status EnQueue(SqQueue *Q, ElemType e){
    if((Q->rear + 1) % MAXSIZE == Q->front){
        return ERROR;   //队满
    }
    Q->data[Q->rear] = e;   //将元素e赋值给队尾
    Q->rear = (Q->rear + 1) % MAXSIZE;  //rear指针向后移一位置，若到最后则转到数组头部
    return OK;
}

出队

/*若队列不空，则删除Q中队头元素，用e返回其值*/
Status DeQueue(SqQueue *Q, ElemType *e){
    if(isEmpty(Q)){
        return REEOR;   //队列空的判断
    }
    *e = Q->data[Q->front]; //将队头元素赋值给e
    Q->front = (Q->front + 1) % MAXSIZE;    //front指针向后移一位置，若到最后则转到数组头部
}

（3）队列的链式存储结构

队列的链式存储结构表示为链队列，它实际上是一个同时带有队头指针和队尾指针的单链表，只不过它只能尾进头出而已。

在这里插入图片描述

空队列时，front和real都指向头结点。

在这里插入图片描述

链队列存储类型

/*链式队列结点*/
typedef struct {
    ElemType data;
    struct LinkNode *next;
}LinkNode;
/*链式队列*/
typedef struct{
    LinkNode *front, *rear;    //队列的队头和队尾指针
}LinkQueue;

当Q->front == NULL 并且 Q->rear == NULL 时，链队列为空。

链队列初始化

在这里插入图片描述

void InitQueue(LinkQueue *Q){
    Q->front = Q->rear = (LinkNode)malloc(sizeof(LinkNode));    //建立头结点
    Q->front->next = NULL;    //初始为空
}

链队列入队

在这里插入图片描述

Status EnQueue(LinkQueue *Q, ElemType e){
    LinkNode s = (LinkNode)malloc(sizeof(LinkNode));
    s->data = e;
    s->next = NULL;
    Q->rear->next = s;    //把拥有元素e新结点s赋值给原队尾结点的后继
    Q->rear = s;    //把当前的s设置为新的队尾结点
    return OK;
}

链队列出队

出队操作时，就是头结点的后继结点出队，将头结点的后继改为它后面的结点，若链表除头结点外只剩一个元素时，则需将rear指向头结点。

在这里插入图片描述

/*若队列不空，删除Q的队头元素，用e返回其值，并返回OK，否则返回ERROR*/
Status DeQueue(LinkQueue *Q, Elemtype *e){
    LinkNode p;
    if(Q->front == Q->rear){
        return ERROR;
    }
    p = Q->front->next;    //将欲删除的队头结点暂存给p
    *e = p->data;    //将欲删除的队头结点的值赋值给e
    Q->front->next = p->next;    //将原队头结点的后继赋值给头结点后继
    //若删除的队头是队尾，则删除后将rear指向头结点
    if(Q->rear == p){    
        Q->rear = Q->front;
    }
    free(p);
    return OK;
}

Share on

X (formerly Twitter) Facebook LinkedIn

Jiacheng Han

DS-Stack and Queue

（一）栈

1、基本概念

2、栈的存储结构

（1）静态顺序存储

进栈（push）

* 共享栈

（2）链式存储

3、栈的运用

（二）队列

1、基本概念

2、队列的顺序存储结构

（1）顺序队列

（2）循环队列

数据类型

初始化

判空

返回长度

入队

出队

（3）队列的链式存储结构

链队列存储类型

链队列初始化

链队列入队

链队列出队

Share on

You May Also Enjoy

【PIN】Bugs

Machine Learning Review

DS-String

CO-Representation and Computation of Data